Marketing Analysis: Unlocking The Power Of Descriptive Statistics
- Fahad H

- Nov 20, 2015
- 5 min read

Let me be up front: this post will contain statistics. Not the fun, pithy kind like “60 percent of statistics are made up on the spot,” but actual cold, hard statistical practices.
Joking aside, I’m going to run through some fairly high-level statistical analysis practices that you can employ every day to help make sense of your marketing data, allowing better strategic decisions. And it won’t be painful at all, I promise.
“But I do this already. I’m always analysing my data!” I hear you say incredulously.
This is probably very true — most users of web analytics (Google Analytics, Omniture, et al.) instinctively apply what would formally be known as “descriptive statistics.”
For example, you readily identify a spike or a drop in your daily traffic by “eyeballing” a chart; you use averages to quickly assess performance; and you do all sorts of comparisons that help you understand what is happening (and importantly, what you need to do next).
Although a loose adherence to the general principles is fine and workable, I strongly believe that an element of rigour can help take your analysis to the next level. Below, I’ll run through a couple of concepts tied to real-world examples that will hopefully convince you that this is an approach you should be considering.
Variance & Standard Deviation
Every set of data has a number of “characteristics” which, when understood, tell you lots about what has happened and what behavior you can expect in the future. One of the major characteristics is the dispersion of data points (i.e., how spread out and different from one another the measurements tend to be).
The formal measure of this is standard deviation (SD), which is derived from its partner metric, variance (σ2). As you’d guess from the names, informally these just represent how much that data can be expected to deviate, and how much it varies. But by utilizing the exact nature of the formal properties, you can do all sorts of fun useful stuff.
The SD is calculated by taking the square root of the variance. To calculate the variance, we just:
Work out the average (mean) of your set of results.
For each measurement you have, subtract the average worked out in step 1, then square the resulting figure. Note each one down.
Add all the numbers you noted when carrying out step two, and voila! The result is your variance.
To get the SD, just take the square root of your calculated variance. So the whole calculation looks like below:
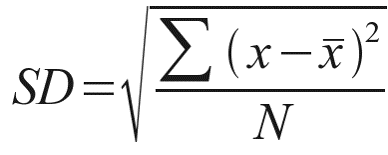
In finance, SD is a key measure of risk or volatility — it’s incredibly useful to know how stable a portfolio of stocks is before investing. A portfolio may have a high average yield and offer great returns, but if it has a high standard deviation, it could be a risky bet that may make you more averse to committing your money to it.
To think of this within the realm of marketing, consider you are allocating monthly budgets across some campaigns. You have these two, which have potential to spend as much of your budget as you’d like:
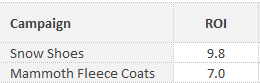
With the pure ROI data, it’s simple: spend everything we can on “Snow Shoes,” and put whatever is left towards the “Mammoth Fleece Coats.” (We’ve had the first snow of the year here today, hence the inspired choice of fake campaigns.)
However, if we crunch the numbers and look at the historical deviations, we’ll get some extra context which, depending on our goals, can allow more strategic thinking:

Now, the “Snow Shoes” campaign is still an attractive option; however, the element of risk/volatility needs to be considered. Is a blended strategy (more of a “balanced portfolio” approach) going to ensure more sensible use of your or your client’s budget? It’s entirely dependent on the situation, but this additional data puts you in a much better position to make sound, informed decisions.
Another action upon seeing this data would be to look into the variance. What is the root cause? Are there actions you can take to lower the SD and maintain high performance?
Standard Deviation & Expectations
In my introduction, I mentioned that it’s highly likely that you’ve identified upward and downward trends by looking at the time-series charts of your chosen analytics package.
Following through with the formal approach, we can use SD to provide the context around these trends and make really informed decisions by sticking to principles.
In distributed data, we can use the number of standard deviations as a benchmark of how “expected” a certain measurement is — e.g., if we simplify and assume daily transaction data is normally distributed (it probably isn’t, but it’s convenient for me to make this assumption here) then 68 percent of all measurements should fall within one standard deviation, whilst 95 percent should fall within two standard deviations.
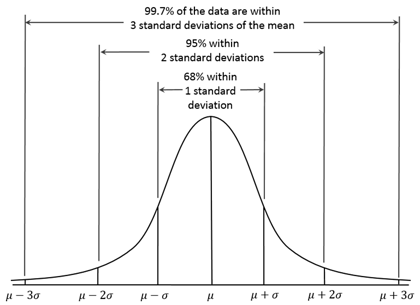
What’s the purpose of knowing this? With limited time on our hands as marketers, we need to pick our battles. Using these expectations as yardsticks allows us to categorize spikes and dips as either “business as usual” or “hmm, that’s interesting, I should probably invest time looking into this one.”
Coming full circle and applying this new context to a time series results in what you see below — firstly, a simple standard deviation calculated across the given period, and secondly, a rolling calculation that ensures ongoing updates of the mean and standard deviation.
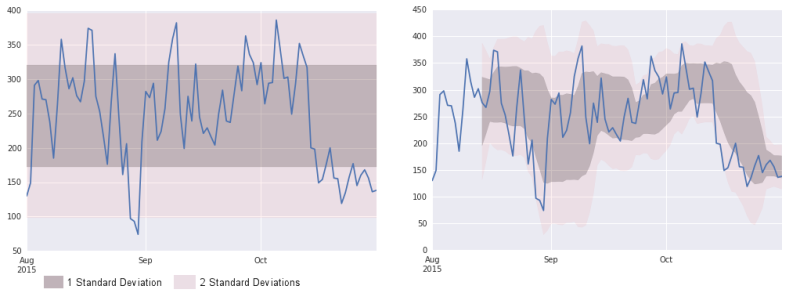
In our first chart, the end of October shows a consistent dip into the “2 Standard Deviations” zone, so we should be looking into why this is the case. Also, we need to know what happened at the end of August — what can we learn here?
Statistical Significance: How Confident Are You?
A familiar one to the conversion optimizers out there, Statistical Significance is a handy method to inform us if a result we are looking at is caused by some definite relationship, rather than just a quirk of randomness within the data.
For example, when A/B testing and making changes aimed at improving a site conversion rate, you need to be certain* that any measured improvements are attributable to your changes and that the perceived result is not just the data pulling the wool over your eyes.
*Certainty is also a defined measure. You can rarely be 100 percent certain, but you may set your goal to be 95 percent certain that improvements are a result of your awesome site redesign and be happy with that.
Following are the key components that affect how significant a result is:
Sample Size: If you’ve measured something lots and lots of times, you can be more certain about your results. Consider if you have two SEOs and a basketball player in a room, your sample size of three leaves you with very little confidence about the average height of a person. If you measure the height of 1,000 people at random, you’ll be much more certain about how true your estimate of average height is. (It’s not been skewed by the unexplained presence of a Chicago Bull attending your SEO meeting.)
Standard Deviation: I hope I’ve succeeded above in conveying what this is. However, the raw SD is not the end of the story. Combining it with the number of measurements (sample size) allows us to calculate the “standard error of the mean (SE).”
The detail of this calculation isn’t important here and now. What I want you to take away from this is that many of the results you are looking at can have a degree of certainty (or uncertainty, if you are a pessimist) and that this uncertainty is reliant on how many times you’ve measured something and how varied the results are when you measure them.
This is relevant, for example, when reviewing:
paid search or programmatic display ad performance.
the success of an email marketing campaign.
social engagement rates with different types of content.
The bottom line is that before making decisions based on data, you should understand your level of certainty and how much you can rely on the figures you are looking at.
Conclusion
I hope this has been useful to those who have not encountered these concepts before, and that you’d agree with me that these extra steps and practices are relevant to our work in search marketing.
I’d consider this to be the tip of the iceberg in what I consider to be an exciting, ongoing challenge: making the data tell a story.




Comments